In part 3 I did some spelunking through the US social security name dataset. In this post I’ll continue to use that data to explore what names have been chosen in the space of possible names.

This is part 4 in the series about searching for a name for this cool cat:

What fraction of possible names actually get used?

Taking 2-letter names for example, it’s easy to show all the 2-letter names that have been used for human names in the US Social Security data:

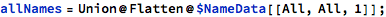
That’s the complete list. Some of these are familiar to me, like “Bo” and “Al”, but many are unfamiliar to me, like “Tr” and “Ah”.

How many possible 2-letter names are there? Well there are 26 letters in the English alphabet, so each of the two letters has 26 possibilities. For the first letter, there are 26 choices, and once you’ve made a choice for the first letter, there are 26 possibilities for the second letter. That means there are

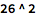
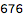
possible 2-letter names.

Of those 676 possible names, 148 of them are present in the database:

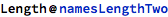
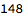
That’s about 22%:

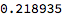
So 78% of the possible 2-letter names have never been used.

It’s easy to show the full space of 2-letter names by just enumerating all possibilities for the first and second letter, and showing them all in a 26 x 26 grid. Here they all are, with the ones that have been used highlighted in yellow:

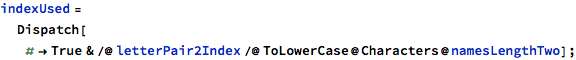
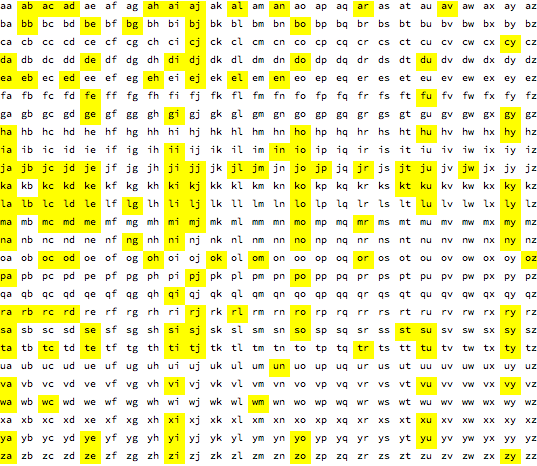
So the name “Ji” is used, but not the name “Oy”? And “Tc” is used, but not “Uz”?

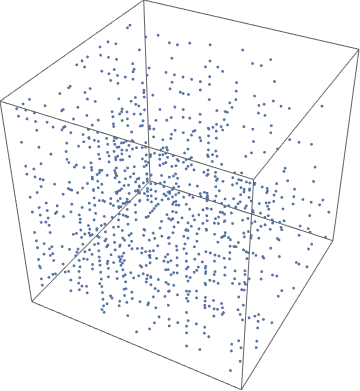
If we go up to three-letter names, they form a 3-dimensional space now:

With 3 letters there are

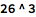
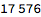
(~17k) possible names. But only

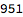
of them appear in the name database. That’s just 5% of the possible 3-letter words:

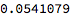
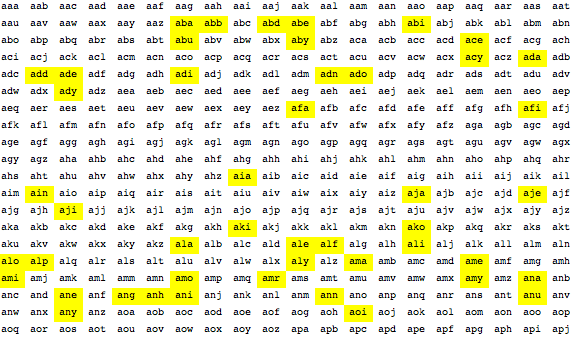
Here are all the 3-letter names used:

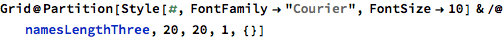
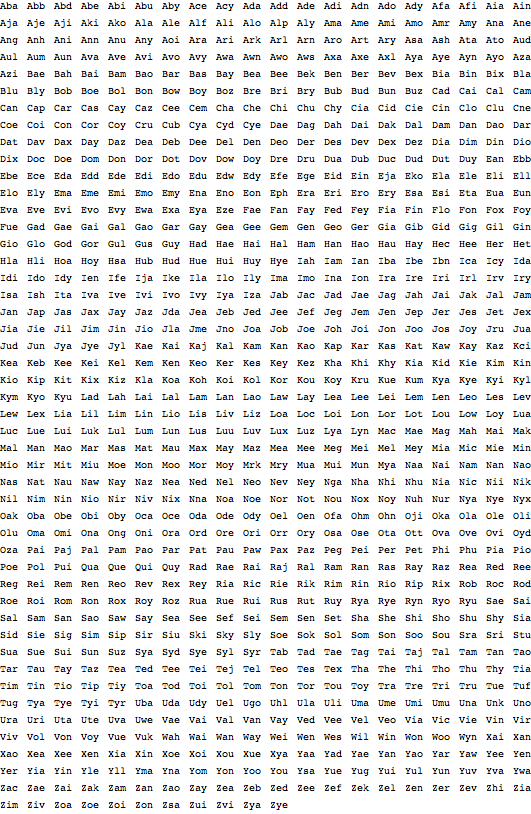
Here’s the beginning of the full space of all 17k possible 3-letter names, with actual names highlighted again:

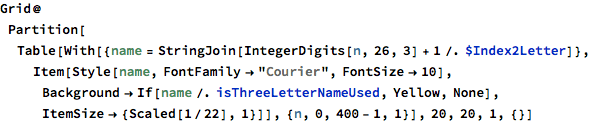
We can get a sense of the density of the space of 3-letter names by plotting them in a grid, with a black cell appearing whenever a name appears in the database:

At just 5% of the possible 3-letter words used for names, the space of 3-letter names is much more sparsely populated than the 2-letter names were.

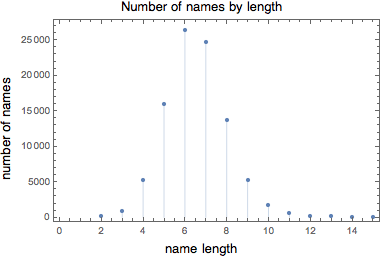
By breaking the database up by name length, we can see how many names of each length there are:

Now for each length let’s compare the number of given names to the total number of possible names (26^n where n is the name length):

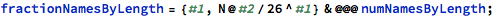
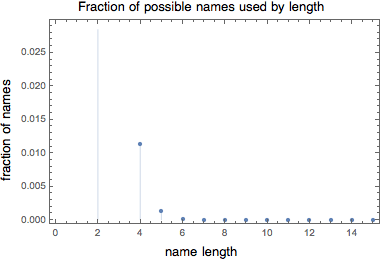
The number of names that get used becomes a vanishingly small fraction of the space of possibilities as the length of the name increases.

The number of names that get used becomes a vanishingly small fraction of the space of possibilities as the length of the name increases.

So even for names with 6 letters, for which there are the most given names overall, only about 0.01% (a hundredth of a percent, or 1 in 10,000) of possible names have been used.

If we wanted to name our son with a 2-letter name, we could easily survey the full list of 676 possibilities. If we wanted a 3-letter name, it would already be pretty difficult if not impossible to consider all 17,576 possible names. But even at 4 letters – which is still a short first name – it’s basically hopeless. There’s no way we could look through all 26^4 = 456,976 names.

So in order to consider new names, I need some way of suggesting candidate names from the huge space of possibilities. It’s a needle in a haystack problem.