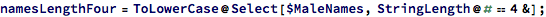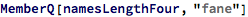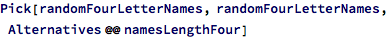So far I’ve failed to capture some structure that makes a string of letters feel like a given name. Somehow being pronounceable isn’t sufficient for being a meaningful name. It feels like I need to find patterns in the given names from the social security data.

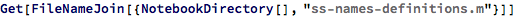
One of the obvious things that is wrong with the randomly generated names is that in names like “vndt” or “ojuq”, the sequence of letters don’t follow typical conventions in English words, like vowels being close to consonants, and certain letters occurring together often.

Taking the name “ojuq” as an (particularly Klingon-sounding) example, how often is the letter “o” followed by the letter “j” in given names? To find out, I can deconstruct all the names in the SS data into letter pairs, and isolate all the pairs starting with the letter “o”. Then I can tally up all the pairs and rank them by frequency. Here’s the result:

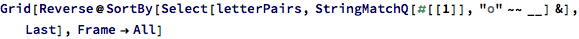
The most popular pairs starting with “o” are “on”, “or”, and “ol”, occurring thousands of times each. The pair “oj” is way down in the second-to-last position, occurring only 55 times in total. So it makes sense that a randomly generated name with the pair “oj” in it might sound unfamiliar to my ear. I’m simply not accustomed to hearing the letter “o” followed by a “j” in given names.

So I should try taking these pair frequencies into account when generating new names, so “oj” will only appear rarely, and “on” and “or” appear much more often.

A good way to take these pair frequencies into account is to generate new names using a Markov sequence. In a Markov sequence, the next item in the sequence depends on what the previous item was.

Taking the “o” pairs above, the pair frequencies can be written down slightly differently:

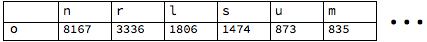
Starting with the letter “o”, this gives a table of counts for the next letter in given names. Now we can convert these to frequencies by dividing each count by the row’s total:

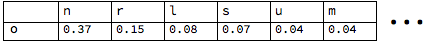
So to make a sequence of letters sound more like a name, “o” should be followed by “n” 37% of the time, “r” 15% of the time, “l” 8% of the time, and so on.

Doing the same for each starting letter in the alphabet, I get a table of transition frequencies for each letter:

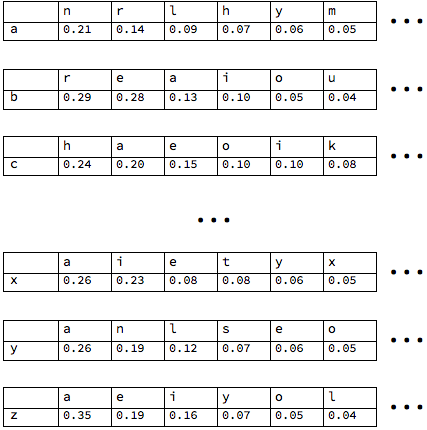
If I sort each table alphabetically instead of descending frequency, I can line all the columns up, and I get a transition matrix:

Plotting the transition matrix using gray levels to indicate the values between 0 (white) and 1 (black) makes the overall structure more clear:

The Markov sequence uses this transition matrix to make a weighted random choice for each letter in the sequence.

So now that we have this model for generating new names, we can generate a new set of names with 4 letters: